Hey there, this is

Chris Pyle

Student and Software Developer

at Northeastern University

Projects

Ski Racing Bib Recognition

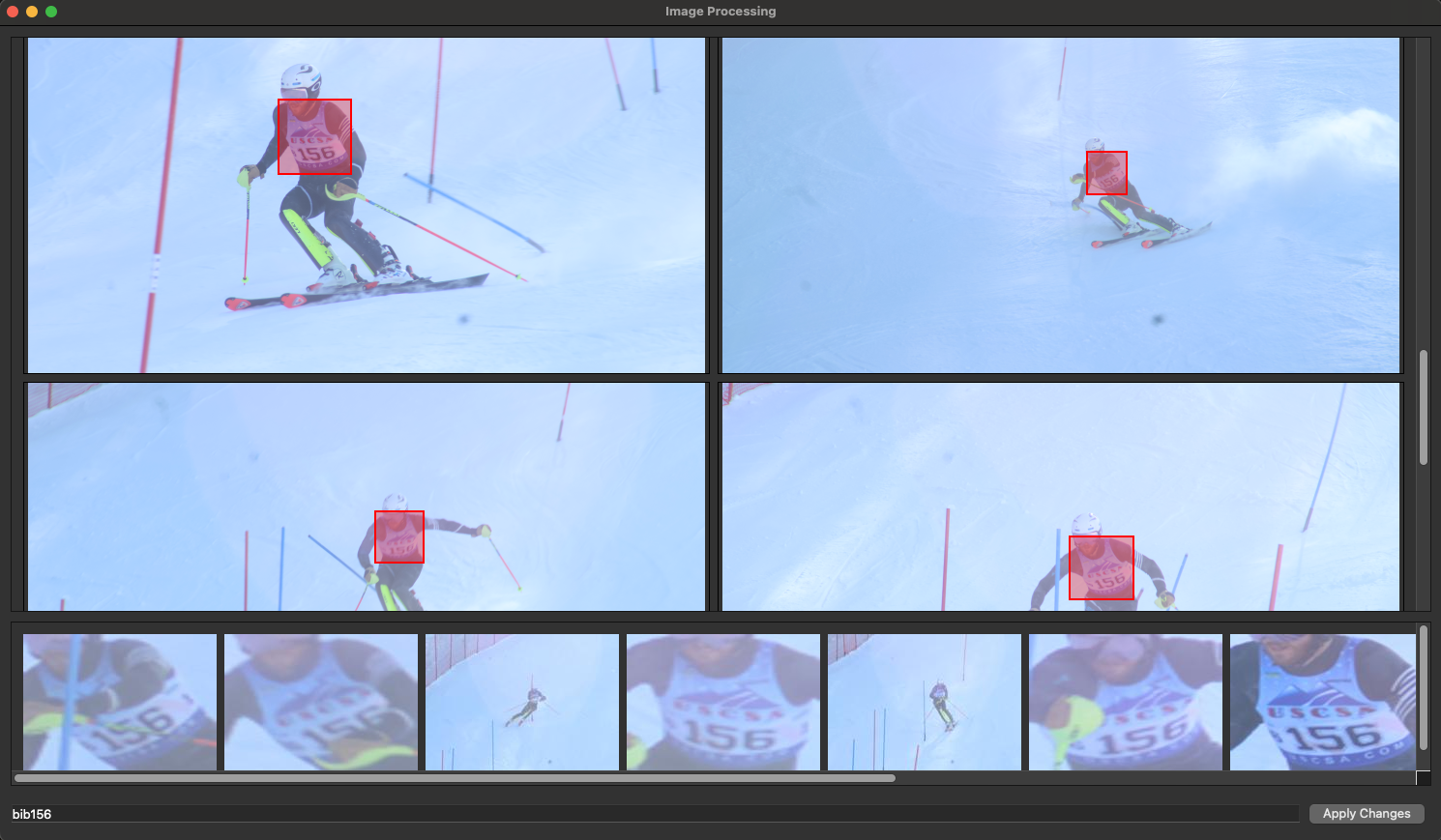
Custom Machine Learning Model and UI to Recognize Bibs and Bulk Sort Images by Racer and Team

PythonMachine LearningYOLO

View on GitHub

Interactive File Review System

Version Management and Markup System For Users to Review and Approve CAD Part Drawings

ReactTypescriptPrisma

View on GitHub

Bitboard Chess Engine

Bitboard Chess Engine in C with Alpha Beta Pruning, Search Extensions, and Positional Evaluation

CGolangAlgorithmsWebsockets

View on GitHub

Image Compressor

Uses Seam Carving Algorithm to Compress Images While Losing Minimal Information

JavaDynamic ProgrammingAlgorithmsDeques

View on GitHub

Ecuadorian Store Sales Forcasting

Time Series Machine Learning Model to Predict Store Sales in Ecuador Using XG Boost

PythonMachine LearningData Analysis

View project details

Maze Generator and Solver

Visually Displays Kruskal's Algorithm to Generate Mazes and DFS/BFS to Solve Them

JavaAlgorithmsData Structures

View on GitHub

Convolutional Neural Network

Multi-Layered Network Built From Scratch Using only NumPy to Classify Handwritten Digits

PythonMachine LearningMathematics

View project details

Delta Kappa Epsilon Website

Recruitement website for the Delta Kappa Epsilon fraternity at Northeastern University

NextJSReactTailwindCSS

View on GitHub

Three Trios Card Game

Multiplayer Card Game with AI Opponents and Swappable UI

JavaObject Oriented DesignMVC PatternAI

View on GitHub

Weight A Minute -- Fitness Tracker

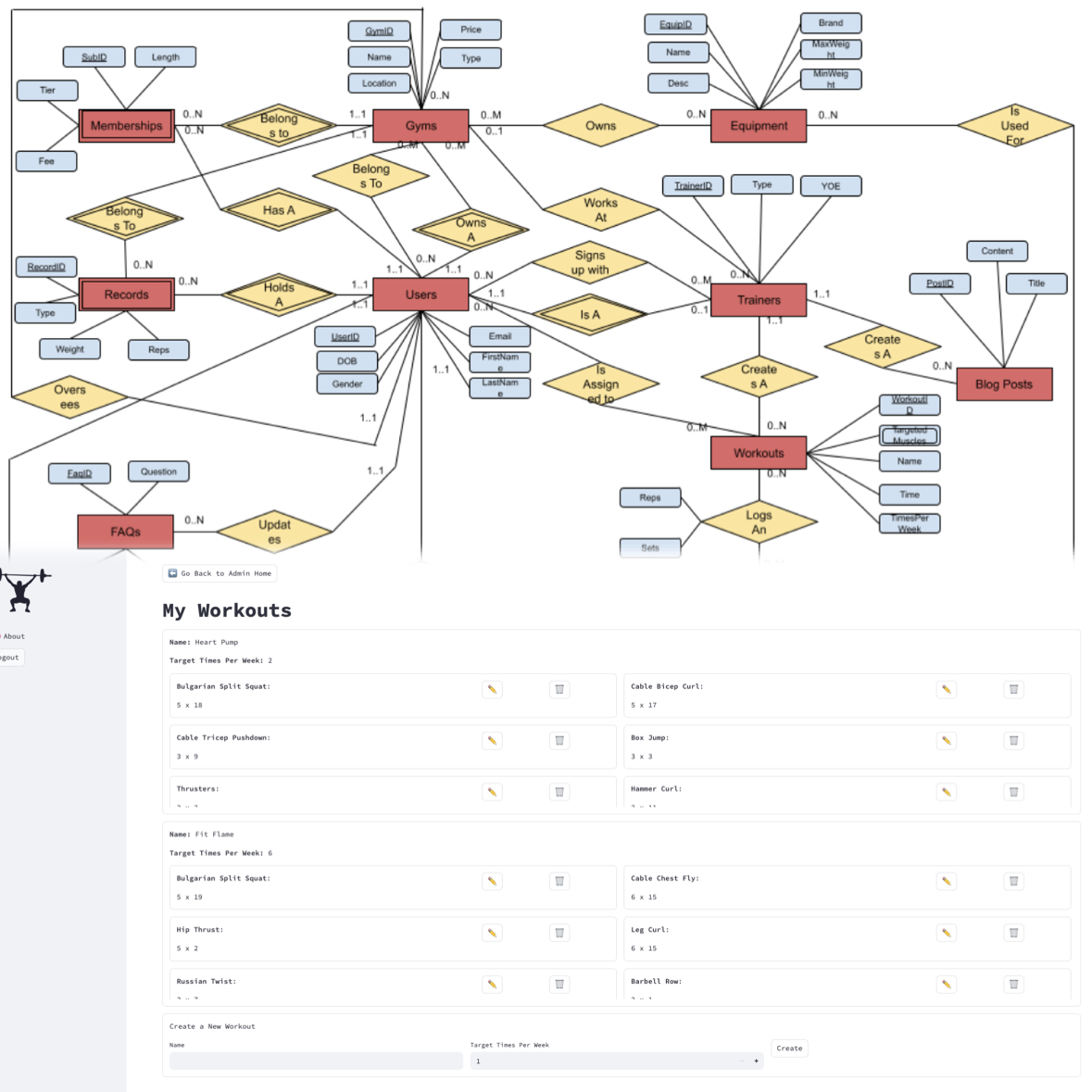
Fitness Tracker Connecting Trainers and Users Providing Workouts Based on User's Gym Equipment

SQLDatabase DesignPython

View on GitHub

Rush Hour Game

Classic Puzzle Game with Reversable Moves, Customizable Levels, and Swappable Rulesets

JavaObject Oriented DesignGame Development

View on GitHub

About

I'm a third-year student studying computer science with a mathematics minor at Northeastern University, with plans to graduate in spring 2027. I recently completed a Co-op at NExT Consulting building a WMS for Via Separations, and I am currently working as the head of web development at Northeastern Electric Racing where I lead the development of Finishline, our custom ERP solution. Additionally, I am a regular volunteer at The Unicode Consortium, writing code for their Adopt A Character program, and am the treasurer for the Alpine Ski Team. Currently, I am learning C and FreeRTOS to contribute to the embedded codebase at NER. I am always looking for ways to write software that solves real problems, whether that be warehouse management at a biotech company or bib detection for ski racing photographers. Non-technically, you will find me on the slopes of ski mountains, hiking through the woods, or in an obscure coffee shop in Boston!

Timeline

2022

2023

2024

2025

Alpine Ski Racer

Gould Academy: September 2010 - Present

extracurricular

I have been alpine ski racing since I was 6 years old, with my journey peaking in high school where I competed at the international level with sub 90 FIS points in slalom and giant slalom

Software Developer Intern

Unicode: August 2022 - September 2023

employment

During my first internship with Unicode, I worked on renewing the adopt a character site with integrations for payment processing as well as external donor databases. Go Adopt a Character!

Computer Science Club Co-Founder

Gould Academy: September - September 2022

extracurricular

During my senior year I co-founded the gould computer science club where we taught students basic programming and robotics skills.

Bill Taylor Essay Contest Winner

Camden Conference: April - April 2023

award

In my essay 'Assessing Internet Inequality in the US', I analyzed the effects of internet inequality and argued for regulations and legislation that could help this pressing issue. Read more here.

Graduation

Gould Academy: May - May 2023

education

I graduated Gould Academy as salutatorian, putting an official end to my 12 year competative alpine ski racing career.

Senior Camp Counselor

Camp Ketcha - Scarburough ME: May - September 2023

employment

As a camp counselor, I enjoyed working with a wide range of ages and interests as I ran many different specialty camps and overnight excursions. I earned rookie counselor of the year for these efforts.

Began Attending Northeastern

Northeastern University: September 2023 - Present

education

In september of 2023 I began my journey at northeastern, which will take 5 years and 3 co-ops.

Software Developer

Electric Racing Club: January - January 2024

extracurricular

During the second semester of my freshmen year, I joined NER as a software developer, working on backend and frontend tickets for our websites home page.

Lead Backend Developer

Unicode: May - September 2024

employment

Returning to unicode, I worked mostly in the backend to automate the adoption process, working with social media sites, mailing systems, manual approvals, and badge processing.

Coding Coach and Brand Ambassador

CodeWiz - Westford Ma: May - August 2024

employment

Taught children ages 7-13 a variety of programming languages and skills including python, java, scratch, and robotics. Additionally represented brand at marketing events by recruiting potential new members.

Fundies 1 TA

Northeastern: September - December 2024

employment

For my first TA job, I went back to the basics with the fundamentals of computer science 1 accelerated section, where I helped students by facilitating office hours, running labs, and providing feedback.

Technical Lead

Electric Racing Club: January - June 2025

extracurricular

In the Beginning of my sophomore year, I was promoted to tech lead, where I oversee a team of developers to design and produce features on a semesterly basis, such as a part review system where users can mark up pdfs!

Coach / Photographer / Secretary

Northeastern Ski Team: January 2025 - Present

extracurricular

After 4 acl tears in my left knee, I decided to move to an advisory role on the club ski team, where I use my skiing, organizational, and photgraphy skills to continue helping the team.

Fundies 2 TA

Northeastern: January - April 2025

employment

Following the bonds made with students from my previous semester TA-ing, I continued my journey in the accelerated section of fundies 2.

Software Engineer

Via Separations: June - December 2025

employment

During my first co-op at Via Separations, I designed and implemented a full stack warehouse management system to track inventory. The system increased accuracy from 50% to 95% for over 10,000 items while also providing full tracability and efficient user workflows.

Head of Web Development

Electric Racing Club: September 2025 - Present

extracurricular

After working as a tech lead for a year, I was promoted to the head of web development, where I manage all development and technical operation of our custom project management site. I lead a team of 8 tech leads and 60+ developers to produce new features every semester!

Resume

Download Resume